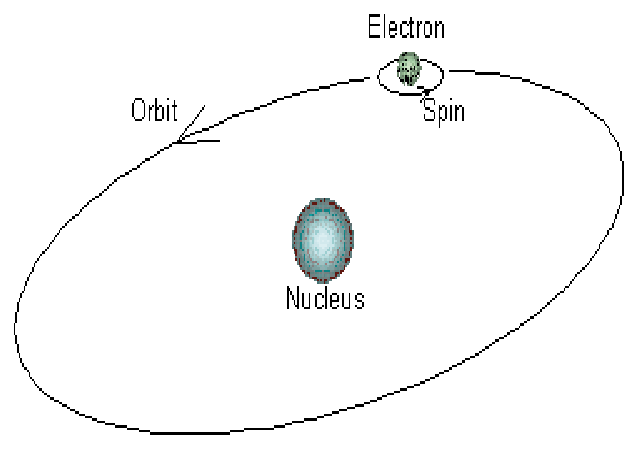
Energy and velocity of Electron

Energy

source : abyss.uoregon.edu

Energy and velocity of Electron-

Calculation for the energy of electron in each orbit –

The energy of a moving electron is the sum of kinetic and potential energy. The total energy of the electron is ‘E’.

KE = 1/2 mv²

Potential energy = – KZe²/r

E = Kinetic energy + Potential energy

= 1/2 mv² – KZe²/r ——– eq 1

We know,

KZe² /r = mv² ———— eq 2

Putting the value of mv2 from eq (2) to eq (1)

E = KZe² /2r – KZe²/r = -KZe²/2r

We know,

r = n²h²/4 $π 2 me 2 KZ$

so,

E = (-KZe² x 4 $π 2 me 2 KZ$ /2 n² h²) = – 2 K²Z² $π 2 me 4 /n 2 h 2$

For H-atom, Z=1

therefore,

E = – 2 K² $π 2 me 4 /n 2 h 2$

h = 6.625 x 10^-34 , $π = 3.14 , m = 9.1 x 10 -31, e = 1.6 x 10 -19, K = 9 x 10 9 Nm 2 /C 2$

putting the values of $π , m , e, K , and h,$

E = – 2 x $9 x 10 9 x 9 x 10 9 x 3.14 x 3.14 x 9.1 x 10 -31 x (1.6 x 10 -19) 4 / n 2 x 6.625 x 10 -34 x 6.625 x 10 -34$

E = -21.70 x 10^-19 / n² joule

For ,n=1 , E = – 21.70 x 10^-19 / 1 x 1= – 21.70 x 10^-19 J = – 21.70 x 10^-12 erg = -13.6 eV

If, n=2 , E = – 21.70 x 10^-19 / 2 x 2= – 5.42 x 10^-19 J

For n=3 , E = – 21.70 x 10^-19 / 3 x 3= – 2.41 x 10^-19 J

Energy of an electron in lower orbit (n₁) and higher orbit(n₂)-

E_n1 = – 2 K²Z² $π 2 me 4 /n 12 h 2$

For H – atom,

Z =1

E_n1 = – 2 K² $π 2 me 4 /n 12 h 2$

E_n2 = – 2 K² $π 2 me 4 /n 22 h 2$

E_n2 – E_n1 = – 2 K² $π 2 me 4 /n 22 h 2 +$ 2 K² $π 2 me 4 /n 12 h 2$

Δ E = (2 K² $π 2 me 4 / h 2)[( 1/ n 12) - ( 1/ n 22)]$

According to Planck’s relation,

Δ E = hc/λ

hc/λ = (2 K² $π 2 me 4 / h 2)[( 1/ n 12) - ( 1/ n 22)]$

1 / λ =( 2 K2 $π 2 me 4 / ch 3)[( 1/ n 12) - ( 1/ n 22)]$

K = 1 in CGS unit

[2 $π 2 me 4 / ch 3] was found to be 1.096 x 10 5 cm -1 which is equal to Rydberg constant “R H “$

1 / λ = R_H $[( 1/ n 12) - ( 1/ n 22)]$

1 / λ = $1.096 x 10 5$ $[( 1/ n 12) - ( 1/ n 22)]$

Calculation of velocity of electron-

According to one postulate of Bohr theory ( Electron can revolve in those orbits whose angular momentum is ‘h / 2 $π’ or its integral multiple).$

mvr = nh/2 $π$

v = nh/2 $πmr ——-eq 1$

We Know,

r = n²h²/4 $π 2 me 2 KZ$

For hydrogen , Z = 1 ,hence,

r = n²h²/4 $π 2 me 2 K ———- eq2$

putting the value of ‘r’ from eq (2) to eq (1)

v = nh x 4 $π 2 me 2 K / 2πmn 2 h 2$

v = 2 $π e 2 K / nh$

h = 6.625 x 10^-34 , $π = 3.14 , e = 1.6 x 10 -19, K = 9 x 10 9 N m 2 /C 2$

v = 2 x 3.14 x $1.6 x 10 -19 x 1.6 x 10 -19 x 9 x 10 9 /n x 6.625 x 10 -34$

Energy and velocity of Electron

Energy and velocity of Electron-