Half life and Average Life Period

Average & half life

source : www.nde-ed.org

Average Life Period & half  life period-

Half Life Period-

“It is equal to the time required to disintegrate half of the quantity of the radioactive element taken”.

or

“Half life period is the time during which half of the quantity of a sample of radioactive element disintegrates.”

Half life is represented by t_1/2. The value of t_1/2  does not depend upon temperature, pressure, catalyst and mass of radioactive substance taken etc.

t_1/2 is a measure of radioactivity and stability of radioactive element.  Greater is the value of t_1/2, greater is the stability of the radioactive element & smaller is its radioactivity.

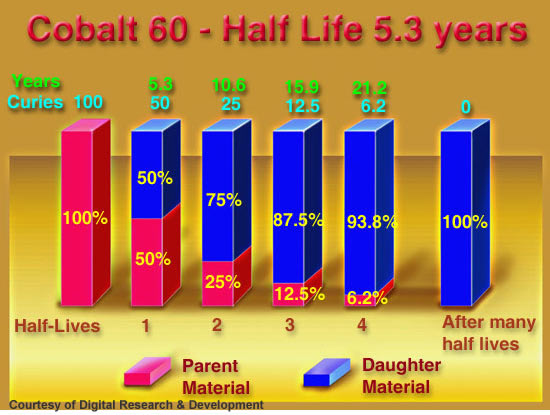
Ex.-      Half life of Ra²²⁶ is 1580 years. This shows that after 1580 years, the mass of radium is half  of the mass taken.

After 2×1580 (=3160 year) the quantity of Ra²²⁶ left will be ¼ ( one fourth) of the mass taken.

Suppose initial mass or no. of atoms of a radioactive element is No.  its half life period is t_1/2

After one t_1/2atoms left = No/2

Atoms left after two half lives = No/4=No/2²

After  three half lives atoms left= No/8 = No/2³

 Atoms left after ‘n’ half lives= No/2ⁿ

The mass or no. of atoms left after ‘n’ half lives is ‘N’

N= No(1/2)ⁿ

T=n×t­_1/2

Relation between disintegration constant and half life-

 Radioactive disintegration is 1^st order reaction . for First order Reaction,

K = ( 2.303 / t ) log a /(a- x) 

If t= t_1/2 ,   & x = a/2 then,

K = ( 2.303 / t_1/2 ) log a /(a- a/2) 

K = ( 2.303 / t_1/2 ) log 2

because , log2 = 0.3010

K = ( 2.303  x 0.3010 / t_1/2 ) 

K = 0.693 / t_1/2

Average Life Period-

 “Reciprocal of t_1/2 of a radioactive element is called its average life period.”

It is represented by τ (Tau)

τ =1/K

K= 0.693 /t_1/2

K = t_1/2 / 0.693

Average life (τ) =1.44×t_1/2