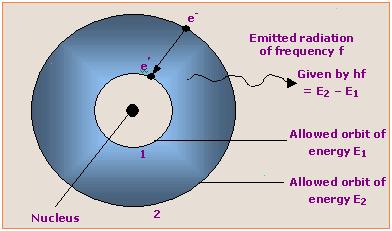
Radius of orbit

source : Hydrogen Atom
Radius of orbit –
Consider an electron of charge ‘e’ revolving around nucleus of charge ‘Ze’,where
Z = atomic number
e = charge on proton
suppose ‘m’ is the mass of the electron and ‘r’ is the radius of the orbit and ‘v’ is the tangential velocity of the revolving electron.
The electrostatic force of attraction between the nucleus and the electron ( according to Coulomb law )
= KZe x e/r2 = KZe2/r2
where , K = 1/4πε0 = constant
Numerical value of K in SI unit = 9 x 109 N m2/C2 but in CGS units K = 1
Centrifugal force acting on the electron= mv2/r
According to Bohr, these two opposing forces must be balancing each other exactly to keep the electron in orbit,
KZe2/r2 = mv2/r
For hydrogen , Z = 1 ,hence,
KZe2/r2 =mv2/r
KZe2 /r = mv2 ———— eq 1
According to one postulate of Bohr theory ( Electron can revolve in those orbits whose angular momentum is ‘h /2 π ‘ or its integral multiple).
mvr = nh/2π
v = nh/2πmr ——–eq 2
putting the value of ‘v’ in eq 1
KZe2 /r = m(nh/2πmr)2
r = n2h2/4π2me2KZ
For hydrogen , Z = 1 ,hence,
r = n2h2/4π2me2K
h = 6.625 x 10-34 , π = 3.14 , m = 9.1 x 10-31, e = 1.6 x 10-19 , K = 9 x 109 Nm2/C2
r = n2 x 6.625 x 10-34 x 6.625 x 10-34 / 4 x 3.14 x 3.14 x 9.1 x 10-31 x 1.6 x 10-19 x 1.6 x 10-19 x 9 x 109
r = 0.529 x 10-10 x n2 metre
radius ‘r’ = 0.529 x n2 Å
r= 0.529 x 10-8 x n2 cm.
The value of ‘r’ for first orbit is called Bohr radius. We can calculate the values of ‘r’ for n = 2 , 3 , 4 etc. orbits of H- atom in excited state.
For n=2 , Then radius of orbit
r= 0.529 x 10-8 x n2 cm = 0.529 x 10-8 x 2 x 2 = 2.12 x 10-8 cm.
For n=3 ,
r= 0.529 x 10-8 x n2 cm = 0.529 x 10-8 x 3 x 3 = 4.76 x 10-8 cm.
For n=4 ,
r= 0.529 x 10-8 x n2 cm = 0.529 x 10-8 x 4 x 4 = 8.46 x 10-8 cm.