source : science20.com
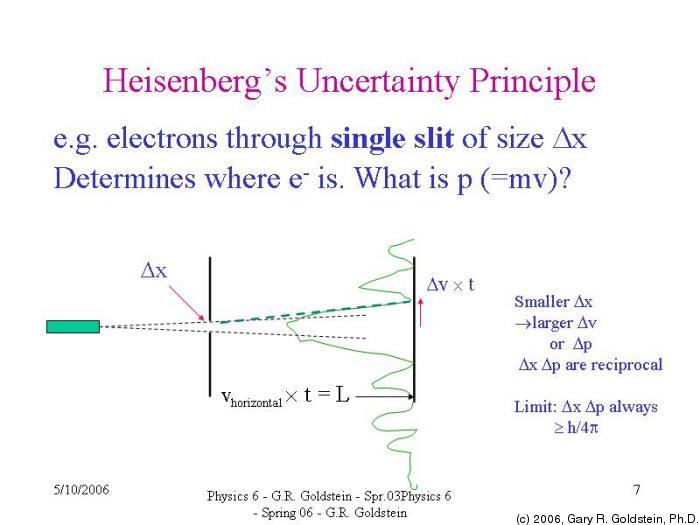
Heisenberg Principle
“It is impossible to measure simultaneously the position and momentum or velocity of a small moving particle with absolute accuracy”.
Heisenberg principle is represented in equation form as follows-
(ΔP)( Δx) ≥ h/4π
ΔP =mΔV
mΔV.Δx ≥ h/4π
ΔV.Δx ≥ h/4πm
Product of uncertainty in position & momentum is greater or equal to h/4π .
Solved Numerical Problems –
Question 1. The mass of an electron is 9.1×10–31 kg. Its uncertainty in velocity is 5.7×105 m/sec. Calculate uncertainty in its position?
Ans. m= 9×10–31
ΔV= 5.7×105 m/sec Δx=?
h= 6.6×10–34 Joule-Sec.
Δx.Δv ≥ h/4πm
Δx ≥ h/4πmΔv
≥ 6.6×10–34/ 4× 3.14 × 9.1 × 10–31 × 5.7 × 105
≥ 0.010×10–8
Δx ≥ 1×10–10m
uncertainty in its position ≥ 1×10–10m
Question 2.The mass of a ball is 0.15 kg & its uncertainty in position is 10–10m. What is the value of uncertainty in its velocity?
Ans. m=0.15 kg. h=6.6×10-34 Joule-Sec.
Δx = 10 –10 m
Δv=?
Δx.Δv ≥ h/4πm
Δv ≥ h/4πmΔx
≥ 6.6×10-34/4 × 3.14 × 0.15 × 10–10
≥ 3.50×10–24 m / sec
uncertainty in its velocity ≥ 3.50×10–24m / sec
Question 3.The mass of a bullet is 10gm & uncertainty in its velocity is 5.25×10–26 cm/sec. Calculate the uncertainty in its position?
Ans. m=10 gm. h=6.6×10–27 erg-sec
Δv = 5.25×10–26 cm / sec
Δx =?
Δx.Δv ≥ h/4πm
Δx ≥ h/4πmΔv
≥ 6.6×10-27/4×3.14×10×5.25×10–26
≥ 0.10×10–2cm
≥ 1×10–3 cm
uncertainty in position ≥ 1×10–3 cm