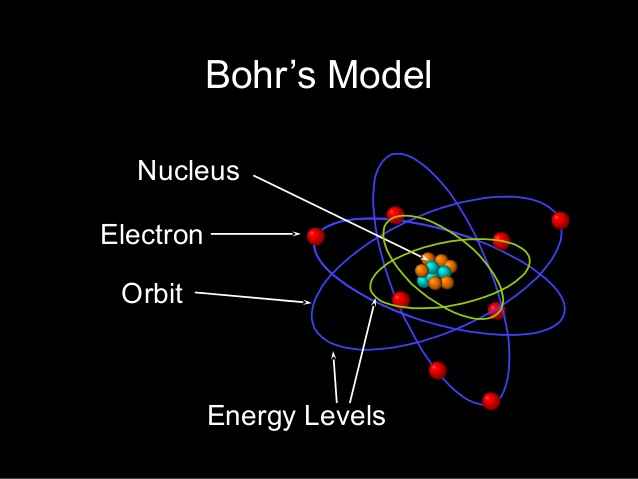
Atomic structure

source: Slideshare.net
Atomic structure- numerical
Question 1) An electron (m = 9.1 x 10-28 gm ) is moving at a velocity of 105 cm/sec. Calculate its kinetic energy and wavelength?
Solution )
m = 9.1 x 10-28 gm , v = 105 cm/sec , h = 6.625 x 10 -27 erg
Kinetic energy = mv2 / 2
= 9.1 x 10-28 x 105 x 105 / 2
K E = 4.55 x 10-18 erg Ans.
λ = h / mv = 6.625 x 10 -27 / 9.1 x 10-28 x 10 5
λ = 0.728 x 10-4 cm -1 Ans.
Question 2) The energies of electron in second and third orbits in hydrogen atom are -5.42 x 10-12 ergs and – 2.41 x 10-12 ergs. Calculate the wavelength of radiation emitted when the electron in a hydrogen atom undergoes a transition from third orbit to second orbit ?
Solution )
E1 = – 5.42 x 10-12 ergs
E2 = – 2.41 x 10-12 ergs
Δ E = E2 – E1 = – 2.41 x 10-12 – (- 5.42 x 10-12)
Δ E = 3.01 x 10 -12 ergs
λ = hc / ΔE
h = 6.625 x 10-27 , c = 3 x 10 10 cm /sec
λ = 6.625 x 10-27 x 3 x 10 10 / 3.01 x 10 -12
wavelength = 6.60 x 10-5 cm Ans.
Question 3) Atomic radius is of the order of 10-8 cm and nuclear radius is of the order of 10-13 cm. Calculate what fraction of atom is occupied by nucleus ?
Solution )
Radius of atom = 10-8 cm
Radius of nucleus = 10-13 cm
volume of atom = 4 π r3/3 = 4 x π x 10-8 x 10-8 x 10-8 /3
volume of nucleus = 4 π r3/3 = 4 x π x 10-13 x 10-13 x 10-13 /3
volume of nucleus / volume of atom = [4 x π x 10-13 x 10-13 x 10-13 /3]/ [4 x π x 10-8 x 10-8 x 10-8 /3]
fraction of volume of nucleus in volume in atom = 10-15 Ans.
Question 4) Calculate the frequency of the spectral line emitted when electron in n = 3 in H-atom de-excites to ground state.
( RH = 109737 cm-1)
Solution )
n1 = 1 (ground state)
n2 = 3
1 / λ = RH [( 1/ n12) – ( 1/ n22)]
λ = c / v
v = RH. c [( 1/ n12) – ( 1/ n22)]
= 109737 x 3 x 1010 [( 1/ 12) – ( 1/ 32)] =
= 329211 x 1010 [( 1/ 1) – ( 1/ 9)]
v = 2.92 x 1015 sec-1 Ans.
Question 5) Calculate the wavelength of radiations emitted producing a line in Lyman series ,when an electron falls from fourth stationary state in H- atom. (RH = 1.1 x 107 m-1)
Solution )
1 / λ = RH [( 1/ n12) – ( 1/ n22)]
For Lyman series , n1 = 1
Given , n2 = 4
1 / λ = 1.1 x 107 [( 1/ 12) – ( 1/ 42)]
1/λ = 1.03 x 107
λ = 0.9708 x 10-7 metre Ans.