Significant figures-

tes.com
Significant figures-
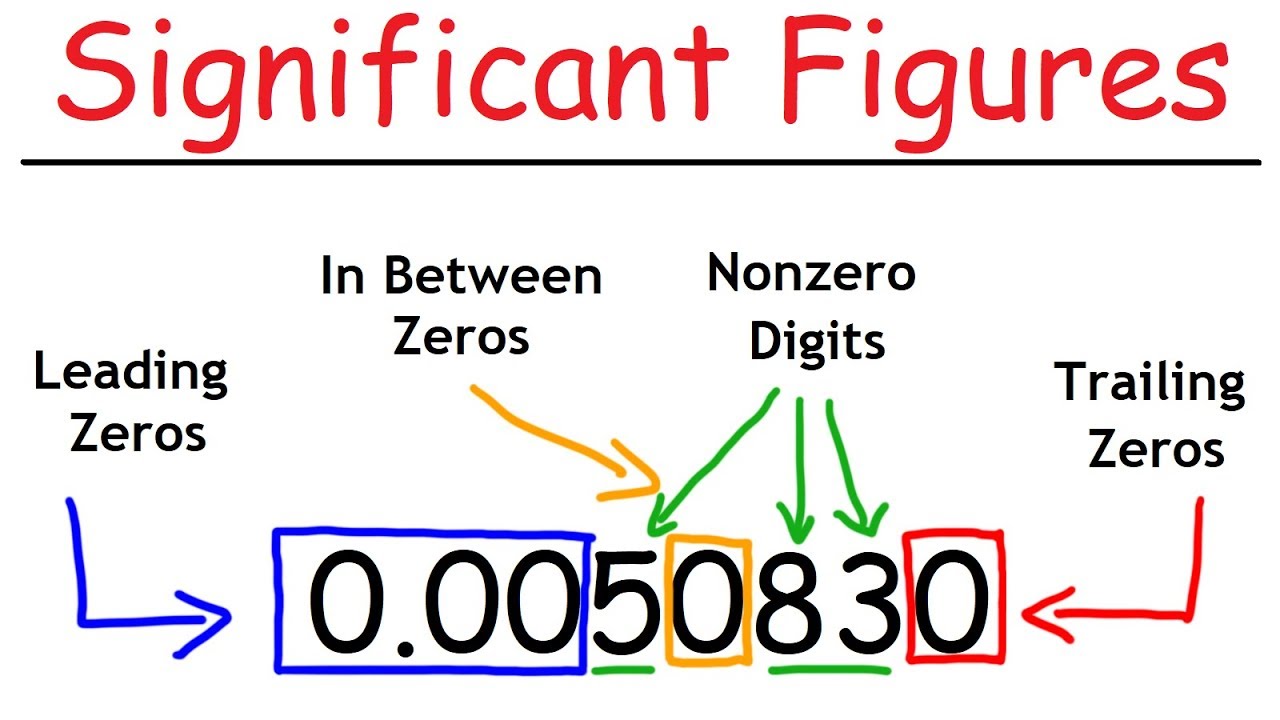
“The significant figures of a number are digits that carry meaningful contributions to its measurement resolution.”
Rules –
1. All non-zero numbers are significant.
Ex – 23.4 has 3 significant figures because all of the digits present are non-zero.
5.146 has 4 significant figures.
2. Zeros between two non-zero digits are significant.
3062 has 4 significant figures. The zero is between 3 and 6
3. Leading zeros are not significant. They represent the position of the decimal.
Ex – 0.054 has only 2 significant figures. All of the zeros are leading.
0.0063 has 2 significant figures.
4. Trailing zeros to the right of the decimal are significant.
67.00 has 4 significant figures.
67.000 has 5 significant figures.
5. Trailing zeros in a whole number with no decimal shown are not significant.
Ex – 650 has 2 significant figures.
1000 has 1 significant figure.
6. Exact numbers have an infinite number of significant figures.
1 meter = 1.00 meters = 1.0000 meters = 1.0000000000000000000 meters, etc.
7. For a number in scientific notation: N x 10n, all digits present in N are significant according to the above rules, the exponential term does not add to the significant figures.
Ex – 2.984 x 103 has 4 significant figures but the exponential term is not significant.
Rule 7 provides an opportunity to change the number of significant figures in the given value by changing its form.
Ex- 1100 has 2 significant figures according to rule 5, its two trailing zeros are not significant. But if we write it in scientific notation that is 1.10 x 103, then it has 3 significant-figures.
Q – How many significant figures are in the following?
a) 3.356 gm
Significant figures= 4
b) 2.3 x 105
Significant figures= 2
c) 0.000169
Significant figures= 3
d) 37.000 gm
Significant figures= 5
e) 6.023 x 1023
Significant figures= 4
f) 1.6 x 10-19
Significant figures= 2