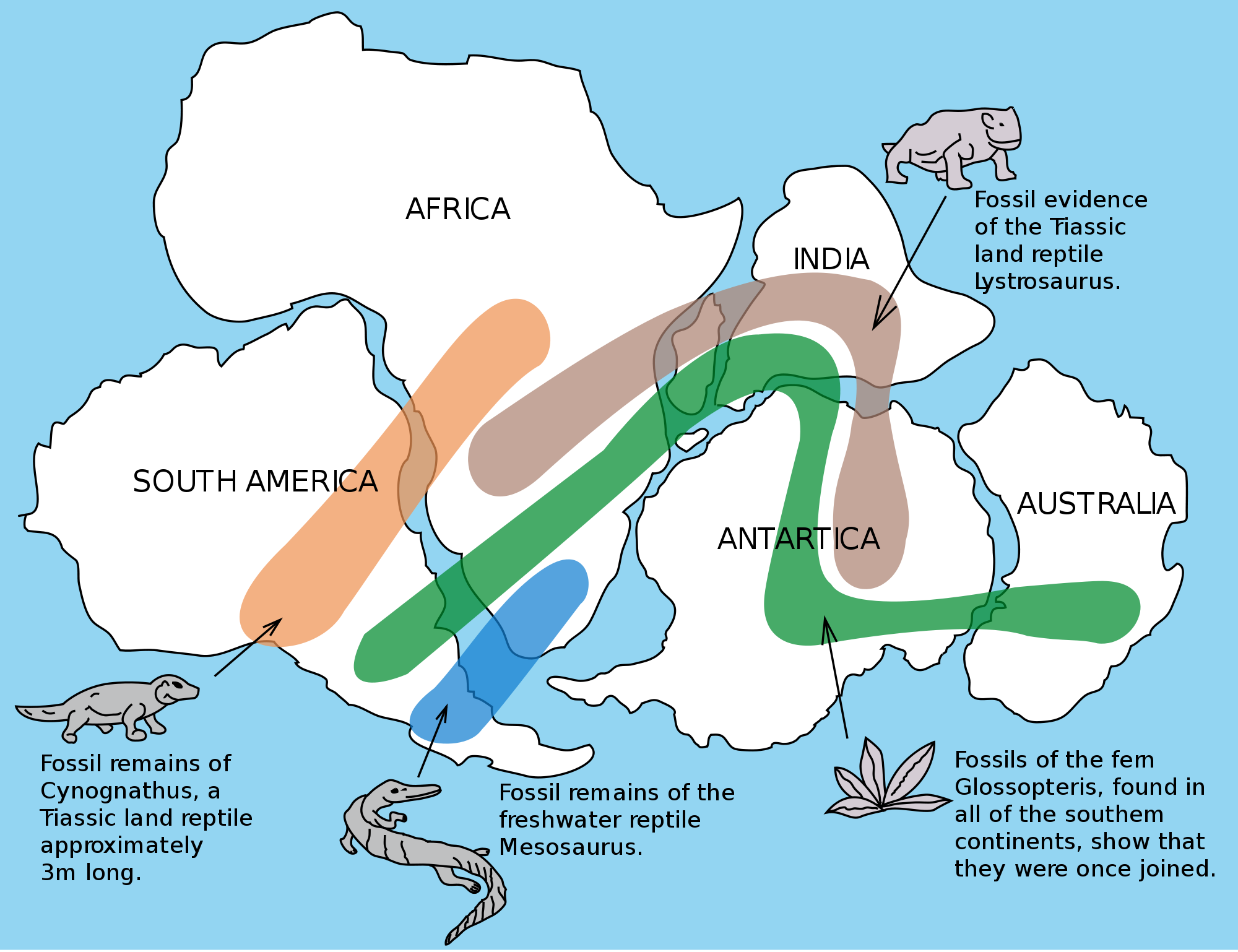
Age of wood and fossil

source : newatlas.com
To calculate the age of wood and fossil or bone-
The age of wood and fossil or bone is determined by Carbon dating method. Activity of C 14 is determined in the leaving plant or animal and then activity of C14 is determined in old wood or fossil. the following formula is used to determine the age of dead animal or plant-
K = (2.303 /t) [log ( activity of C14 in fresh wood or animal / activity of C14 in dead wood or animal )
K = (2.303 / t) [log ( N0 / N )]
Number of atoms of C14 or gram atoms of C14 may be taken in place of activity.
Numerical-
Question 1) The activity of C14 in an old piece of wood is 7 particles per minute. Half life of C14 is 5770 years . The activity of C14 in fresh piece of wood is 14 particles per minute. Calculate the age of wood ?
Solution )
K = (2.303 /t [log) ( activity of C14 in fresh wood or animal / activity of C14 in dead wood or animal )
activity of C14 in fresh wood = 14 particles
activity of C14 in old wood = 7 particles
Age of wood ( t) = ?
t1/2 = 5770 years
K = 0.693 / t1/2 = 0.693/ 5770 = 0.00012= 1.2 x 10-4 years -1
K = 2.303 / t [ log 14 / 7 ]
1.2 x 10 -4 =( 2.303 / t )[ log 2]
t = (2.303 / 1.2 x 10-4 )[0.3010 ] = 2.303 x 0.3010 / 1.2 x 10-4
t ( age of wood) = 5776.7 years Ans.
Question 2) The mass of C14 in wood piece remains 1/16 of the C14 in a living plant. Half life of C14 is 5577 years. Calculate the age of wood?
Solution )
Mass of C14 in living plant / Mass of C14 in wood piece remain = 16 / 1
Means N=1, N0 = 16
t1/2 = 5577 years
K = 0.693 / t1/2 = 0.693/ 5577 = 0.000124 = 1.24 x 10-4 years-1
K = 2.303 /t [log ( N0 / N )]
t = 2.303 / K [ log 16 / 1]
t = 2.303 / K [ log 24 ]
t = (2.303 / 1.24 x 10-4 )[4 log 2 ]
t = (2.303 / 1.24 x 10-4 )[4 x 0.3010 ] = 2.303 x 0.3010 x 4 / 1.24 x 10-4
t ( age of wood) = 22361 years Ans.
Question 3) One of the hazards of nuclear explosion is the generation of Sr90 and its subsequent incorporation in bones . This element has a half life of 28.1 years. If one microgram was absorbed by a new born baby, how much Sr90 will remain in his bones after 20 years?
Solution )
t1/2 = 28.1 years , initial amount ‘N0‘ = one microgram = 10-6 gm , N =? , t = 20 years
K = 0.693 / t 1/2 = 0.693/ 28.1 = 0.0246 years-1
K = 2.303 /t [log ( N0 / N )]
0.0246 = (2.303 / 20)[log 10-6 / N]
0.0246 x 20 / 2.303 = log 10-6 / N
0.2136 = log 10-6 / N
log 10-6 / N =Antilog 0.2136 = 1.635
N = 10-6 / 1.635 = 0.611 x 10-6
Sr90 will remain in his bones after 20 years (N )= 6.11 x 10-7 gm Ans.
Question 4) The half life period of C14 is 5760 years. A piece of wood when buried in the earth had 1 % C14 .Now as charcoal it has only 0.25 % C14 . How long has the piece of wood been buried ?
Solution )
t1/2 = 5760 years , N0 = 1 gm , N = 0.25 gm , t =?
K = 0.693 / t1/2 = 0.693/ 5760 = 0.00012 = 1.2 x 10-4 years-1
K = (2.303 /t) [log ( N0 / N )]
t = 2.303 / K [ log 1 /0.25]
= 2.303 / K [ log 4]
t= 2.303 / K [ log 22 ]
= (2.303 / 1.2 x 10-4 )[2 log 2 ]
t = (2.303 / 1.2 x 10-4 )[2 x 0.3010 ] = 2.303 x 0.3010 x 2 / 1.2 x 10-4