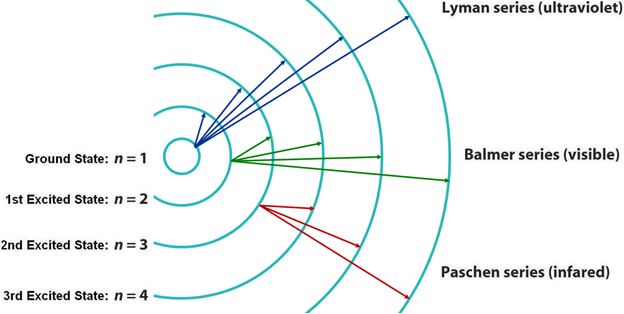
Atomic structure

source : Socratic.org
Atomic structure numerical-
Question 1) The electron energy in H – atom is given by E = -21.7 x 10-12/n2 erg. Calculate the energy required to remove an electron completely from n = 2 orbit. What is the longest wavelength ( in cm ) of light that be used to cause this transition ?
Solution )
E = -21.7 x 10-12/n2 erg
n=2 , then energy of electron ,
E 2= -21.7 x 10-12/(2 x 2)
E 2= – 5.425 x 10-12 erg
Energy of electron completely remove from second orbit, n = ∞
E ∞= -21.7 x 10-12 /∞ 2 = 0
E ∞ = 0
Energy required to remove electron from second orbit completely is,
ΔE = E ∞ – E2 = 5.425 x 10-12 erg Ans.
λ = hc / ΔE = 6.625 x 10-27 x 3 x 1010 / 5.425 x 10-12 = 3.66 x 10-5 cm.
longest wavelength of light which can remove an electron completely from n = 2 orbit is 3.66 x 10-5 cm. Ans.
Question 2) Light of wavelength 12818 Å is emitted when the electron of a hydrogen atom drops from 5th to 3rd orbit. Find the wavelength of the photon emitted when the electron falls from 3rd to 2nd orbit?
Solution)
n1 = 3 , n2 = 5 , λ = 12818 Å
1 / λ = RH [( 1/ n12) – ( 1/ n22)]
1 / 12818 =RH [( 1/ 32) – ( 1/5 2)]
12818 = 25 x 9/16 x RH eq 1
If n1 = 2 , n2 = 3 , λ = ?
1 / λ = RH [( 1/ 22) – ( 1/ 3 2)]
λ = 36 / 5 x RH eq 2
Divide eq (2) by eq (1)
λ / 12818 = 36 x 16 RH / 5 x 9 x 25 RH
λ= 12818 x 64 / 125
λ = 6562.8 Å Ans.
Question 3) The ionisation energy of H- atom is 13.6 eV. What will be the ionisation energy of He+ and Li++ ions ?
Solution )
Ionisation energy = – energy of first orbit
Energy of first orbit of H- atom = – 13.6 eV
Energy of first orbit of He+ = – 13.6 Z2
Z of He+ = 2
Energy of first orbit of He+ = -13.6 x 2 x 2= -54.4 eV
Ionisation energy of He+ = – (-54.4)= 54.4 eV Ans.
Energy of first orbit of Li++ = – 13.6 Z2
Z of Li++ = 3
Energy of first orbit of Li++ = -13.6 x 3 x 3 = – 122.4 eV
Ionisation energy of Li++ = – (-122.4)= 122.4 eV Ans.
Question 4) The wavelength of a certain line in Balmer series is observed to be 4341 Å . To what value of ‘n’ does this correspond ? ( RH = 109678 cm-1)
Solution )
For Balmer series , n1 = 2