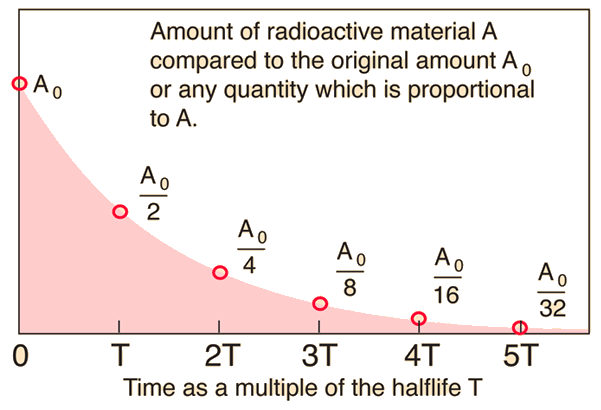
half life
source : www.xraymachines.info
Question 1 ) Half life period of a radioactive element is 10 years. Calculate its disintegration constant & average life?
Ans.
Given, t1/2 =10 years
K = 0.693 / t1/2 = 0.693 / 10
K= 0.0693 years1 Ans
Average life = 1.44 × t1/2=1.44×10
Average life = 14.4 years Ans.
Question 2) Half life period of U234 is 2.5×105 years. In how many years it will remain 25% of original amount?
Ans.
Given t1/2 =2.5×105 years
No = 100 gm
N = 25 grams
N= N0(1/2)n
25 = 100 (1/2)n
25 / 100 =(1/2)n
(1/4 ) =(1/2)n
(1/2)2 =(1/2)n
n=2
T=n×t1/2
= 2×2.5×105
T=5×105 years Ans
Question 3) 10 gram thorium remains 5 grams in 24 days . How much of thorium remains in 48 days ?
Ans –
t1/2=24 days
T=n×t1/2
n =48/24 =2
N= N0(1/2)n
N= 10 (1/2)2
N =2.5 grams
Question 4) Half life of83 I125 is 60 days.How much its radioactivity remains after 180 days ?
Solution )
Given t1/2 = 60 days , T = 180 days
Let initial reactivity ‘No’ = 100 gm
T=n×t1/2
n = T / t1/2
n =180 / 60 = 3
N= N0(1/2)n
N = 100 (1/2)3
=100 (1/8) = 12.5
N = 12.5 % Ans.
Question 5) The activity of a radioactive element remains 12.5% in 90 days. Calculate the disintegration constant of the element ?
Solution )
Given T = 90 days
No = 100 gm
N = 12.5 grams
N= N0(1/2)n
12.5 = 100 (1/2)n
12.5 / 100 =(1/2)n
(1/8 ) =(1/2)n
(1/2)3 =(1/2)n
n=3
T=n×t1/2
90 = 3 × t1/2
t1/2 =90/3 = 30 days
K =0.693 /t1/2 = 0.693 / 30
K = 0.0231 days-1
Question 6) Starting with 16 atoms of a radioactive element , how many atoms are left after 4 half lives?
Solution )
No = 16 atoms
N = ?
n = 4
N= N0(1/2)n
N = 16 (1/2)4
= 16 (1/16) = 1
N = 1 atom Ans.
Question 7) Thorium is 87.5 % disintegrated in 48 days . Calculate the disintegration constant ?
Solution )
Given T = 48 days
N0 = 100 gm
Disintegrated amount = 87.5 gm
Amount of Thorium left ‘N’ = 100 – 87.5 = 12.5 gm
N = 12.5 grams
N= N0(1/2)n
12.5 = 100 (1/2)n
12.5 / 100 =(1/2)n
(1/8 ) =(1/2)n
(1/2)3 =(1/2)n
n=3
T=n×t1/2
48 = 3 × t1/2
t1/2 =48/3 = 16 days
K =0.693 /t1/2 = 0.693 / 16
K = 0.043 days-1 Ans.
Question 8) Half life of 1H3 is 13.3 years. How much of 1H3 should be taken initially so that it remains 4 Kg after 26.6 years ?
Solution )
n= ? , T = 26.6 years , t1/2 = 13.3 years
T=n×t1/2
n = T / t1/2 = 26.6 / 13.3 = 2 half lives
N = 4 Kg , N0 = ?
N= N0(1/2)n
4 = N0 (1/2)2
4 = N0 /4
N0 = 16 kg Ans.
Question 9 ) How much of a radioactive element is left after 5 half lives ?
Solution )
Initial amount = N0
Amount left after 5 half lives ‘N’ = ?
n = 5
N= N0(1/2)n
N = N0 (1/2)5
= N0 (1/32) = N0 / 32